霍夫曼編碼(Huffman Coding)
思路:相較於不常出現的物件,以較短的位元數來編碼較常出現的物件。
此法雖然可以編碼任何類型的物件,比較常見還是用於壓縮位元組流(stream of bytes)。比方說,你有以下文字,其中每個字元是占一位元組:
so much words wow many compression
如果計算每個位元組代表的字母出現的頻率,可以發現一些字母發生次數較多:
space: 5 u: 1
o: 5 h: 1
s: 4 d: 1
m: 3 a: 1
w: 3 y: 1
c: 2 p: 1
r: 2 e: 1
n: 2 i: 1
我們可以指定不同的編碼bit strings給不同的字元,例如給較常見字元較短的編碼,例如:
space: 5 010 u: 1 11001
o: 5 000 h: 1 10001
s: 4 101 d: 1 11010
m: 3 111 a: 1 11011
w: 3 0010 y: 1 01111
c: 2 0011 p: 1 11000
r: 2 1001 e: 1 01110
n: 2 0110 i: 1 10000
將每個字元以編碼後bit strings替換,壓縮資料後的輸出為:
101 000 010 111 11001 0011 10001 010 0010 000 1001 11010 101
s o _ m u c h _ w o r d s
010 0010 000 0010 010 111 11011 0110 01111 010 0011 000 111
_ w o w _ m a n y _ c o m
11000 1001 01110 101 101 10000 000 0110 0
p r e s s i o n
在結尾處我們多放一個位元使其成為位元組大小的整數倍。透過霍夫曼編碼(Huffman Coding),將一34位元組的資料壓縮為16位元組的資料,節省了50%的空間。
在此先暫停⋯⋯要解碼這個資料,我們需要有一個頻率表。此表要連同壓縮資料一起儲存或是傳送,否則解碼器無法解讀這些位元資料。因為這項額外的空間,霍夫曼編碼(Huffman Coding)並不適合用於小資料的編碼。
運作原理
當壓縮位元組流時,首先建立一個頻度表紀錄每個位元組出現的頻度,基於此建立一個二元數來描述每個位元組編碼後的bit strings,示意如下:
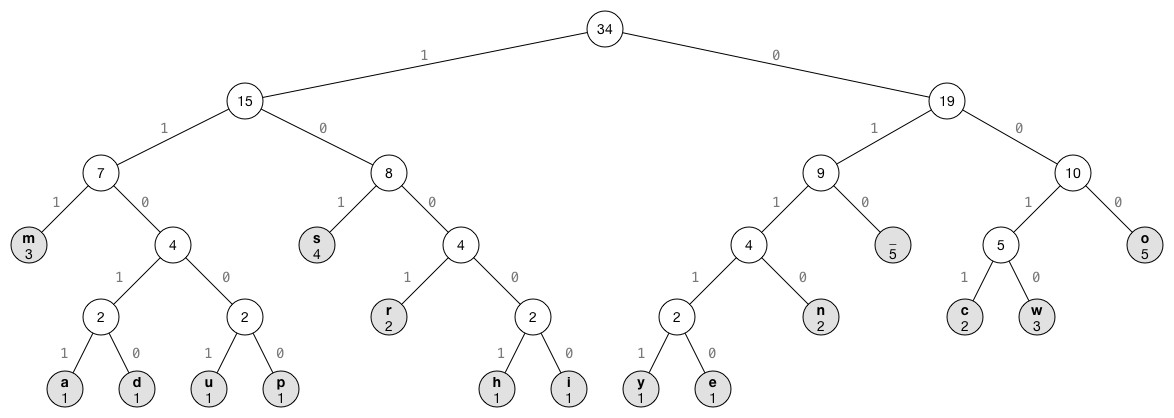
注意此樹有13個灰色的葉子節點,每個代表輸入資料的一個位元組,同時也記錄其頻度,其他的節點為中介節點,其數字代表其子節點的加總,因此跟節點的數字代表輸入資料的位元組數。每個邊旁標示1或0代表對葉子節點的編碼,而左節點是1, 右節點是2。之後的壓縮是循著輸入資料的位元順序字根遍歷至葉子節點的路徑。左邊取1右邊取0。例如由跟節點到c的路徑是右0右0左1左1,因此對c編碼0011。
解壓縮是反向將位元碼反向還原成位元組,讀取壓縮資料的每個位元資料並依位元資訊遍歷樹找到葉子節點代表的位元組,葉子節點的值極為為壓縮的位元組。例如:編碼資料11010,我們從根開始是沿著左左右左右的路徑走,可以找到d。
實作
在實作霍夫曼編碼(Huffman Coding),通常需要幾個可以讀取與寫入NSData物件位元資料的輔助函式,因為在NSData的資料中最小的單元是位元組(byte),而我們需要對位元(bit)做處理,因此需要能夠彼此轉換的方法。
public class BitWriter {
public var data = NSMutableData()
var outByte: UInt8 = 0
var outCount = 0
public func writeBit(bit: Bool) {
if outCount == 8 {
data.appendBytes(&outByte, length: 1)
outCount = 0
}
outByte = (outByte << 1) | (bit ? 1 : 0)
outCount += 1
}
public func flush() {
if outCount > 0 {
if outCount < 8 {
let diff = UInt8(8 - outCount)
outByte <<= diff
}
data.appendBytes(&outByte, length: 1)
}
}
}
呼叫writeBit()來將一個位元加到NSData中。功能是將每個新的位元加到outByte當位元數8時就添加到NSData物件。flush()輔助函式則用來輸出補足壓縮後資料的位元數為8的倍數,會將需要補足的位元以0寫入。同時我們也會需要由NSData中讀取個別位元的輔助函式:
public class BitReader {
var ptr: UnsafePointer<UInt8>
var inByte: UInt8 = 0
var inCount = 8
public init(data: NSData) {
ptr = UnsafePointer<UInt8>(data.bytes)
}
public func readBit() -> Bool {
if inCount == 8 {
inByte = ptr.memory // load the next byte
inCount = 0
ptr = ptr.successor()
}
let bit = inByte & 0x80 // read the next bit
inByte <<= 1
inCount += 1
return bit == 0 ? false : true
}
}
運作方式相似。自NSData中讀取位元組資料,放入inByte變數。呼叫readBit()回傳從位元組中的個別位元,當readBit()被呼叫8次,我們自NSData取下一個位元組。
注意: 如果不熟悉位元操作,不用太在意,只要先知道者兩個輔助函數的功能是在協助我們對位元資料進行讀取與寫入。
頻度分布表(frequency table)
霍夫曼編碼(Huffman Coding)壓縮法的第一個步驟是讀取整個輸入資料流並建立一個頻度表,此表包含256種可能的位元組值及各自在來源資料中的頻度。可以以字典或是陣列來建立頻度表。因為我們要建立一個樹結構,因此不仿直接儲存為葉子。以下是我們需要事先定義的:
class Huffman {
typealias NodeIndex = Int
struct Node {
var count = 0
var index: NodeIndex = -1
var parent: NodeIndex = -1
var left: NodeIndex = -1
var right: NodeIndex = -1
}
var tree = [Node](count: 256, repeatedValue: Node())
var root: NodeIndex = -1
}
我們將樹結構以tree陣列儲存,陣列元素為Node。此為二元樹需要left與right參考回其parent節點。不像典型的二元樹以指標來參考其他節點,此處我們用簡單的整數索引值來建立此tree陣列。(我們也儲存了節點的索引值index在陣列中,其原因後面會說明)。因為每個位元組可能的值有256種,tree陣列的大小為256。當然不是當中所有元素都會被用到,這取決於來源資料。之後我們會新增中介節點在陣列中,以建立完整的樹。目前來說,還不是一棵樹,只是有256個葉子的節點,而節點間還沒有連結。
我們實作下列方法來計算每個位元組出現的頻度:
extension Huffman {
private func countByteFrequency(data: NSData) {
var ptr = UnsafePointer<UInt8>(data.bytes)
for _ in 0..<data.length {
let i = Int(ptr.memory)
tree[i].count += 1
tree[i].index = i
ptr = ptr.successor()
}
}
}
此步驟在NSData物件中由開始到結束,以位元組步進方式一一計算每個葉子在資料中的頻度count,在執行countByteFrequency()完成會記錄256個Node 物件的頻度表於tree陣列中。
先前提過,解碼霍夫曼編碼(Huffman Coding)的資料也需要此表,如果壓縮後的數據是存於檔案中,也需要將頻度表包含於檔案中。
你可以簡單地從tree陣列中的256個元素得到頻度數據,但這樣不是很有效率。這256個元素並不會全部都被用到,再者,節點當中的parent、right與left 指標也不需要,我們只是需要頻度的資訊而非整棵樹。(註記:壓縮資料的目的是節省空間,若為了維護頻度表而佔用太多空間,本身就不合邏輯)
因此,我們實作另一個方法,使我們可以刪除掉沒用的節點又能獲取頻度表的數據:
struct Freq {
var byte: UInt8 = 0
var count = 0
}
extension Huffman {
func frequencyTable() -> [Freq] {
var a = [Freq]()
for i in 0..<256 where tree[i].count > 0 {
a.append(Freq(byte: UInt8(i), count: tree[i].count))
}
return a
}
}
frequencyTable()函式會遍歷一開始的這256個節點,但僅保留實際有用上的,而且只儲存包含位元組值與頻度值的物件Freq,壓縮資料後也要帶上此表使壓縮資料可以正確地被解壓縮。
樹
此例的樹結構如下圖示:

葉子節點代表出現在輸入資料中的一個位元組,若頻度越高的葉子,連接葉子與根之間的中介節點樹越少,例中m、s、空白及o是出現頻度較高的字元,他們在樹比較高的位置。
要建立這棵樹,有以下程序:
- 找兩個還沒有父節點且頻度最低的節點
- 建立一個父節點來連接這兩個節點
- 重複持續到只有一個節點沒有父節點,此節點即成為根節點。
因為我們要重複地找到節點技術值低的節點,這裡是一個使用優先佇列(priority queue)資料結構的好地方,因為它找到最小值非常快速。
實作buildTree()方法如下:
extension Huffman {
private func buildTree() {
var queue = PriorityQueue<Node>(sort: { $0.count < $1.count })
for node in tree where node.count > 0 {
queue.enqueue(node) // 1
}
while queue.count > 1 {
let node1 = queue.dequeue()! // 2
let node2 = queue.dequeue()!
var parentNode = Node() // 3
parentNode.count = node1.count + node2.count
parentNode.left = node1.index
parentNode.right = node2.index
parentNode.index = tree.count
tree.append(parentNode)
tree[node1.index].parent = parentNode.index // 4
tree[node2.index].parent = parentNode.index
queue.enqueue(parentNode) // 5
}
let rootNode = queue.dequeue()! // 6
root = rootNode.index
}
}
分步驟解說如下:
建立優先佇列(priority queue)資料結構並且將所有葉子節點新增進去。
PriorityQueue物件會依其頻度值排序最小的作為第一個被dequeue()的因為迴圈條件式限定至少2個節點在佇列中,因為是最小值自優先佇列,自佇列中移出兩個節點會是沒有父結點且計數最少的兩個。
建立連接
node1與node2兩節點的中介節點,其計數值為兩節點計數值之合,以node1.index與node2.index替代指標來於tree陣列連接節點的左右兩節點。連接兩節點的父節點
再將新建立的中介節點加入佇列中
重複步驟2-5直到佇列中僅剩一節點,此節點即成為樹的根節點
以下動畫顯示其過程:
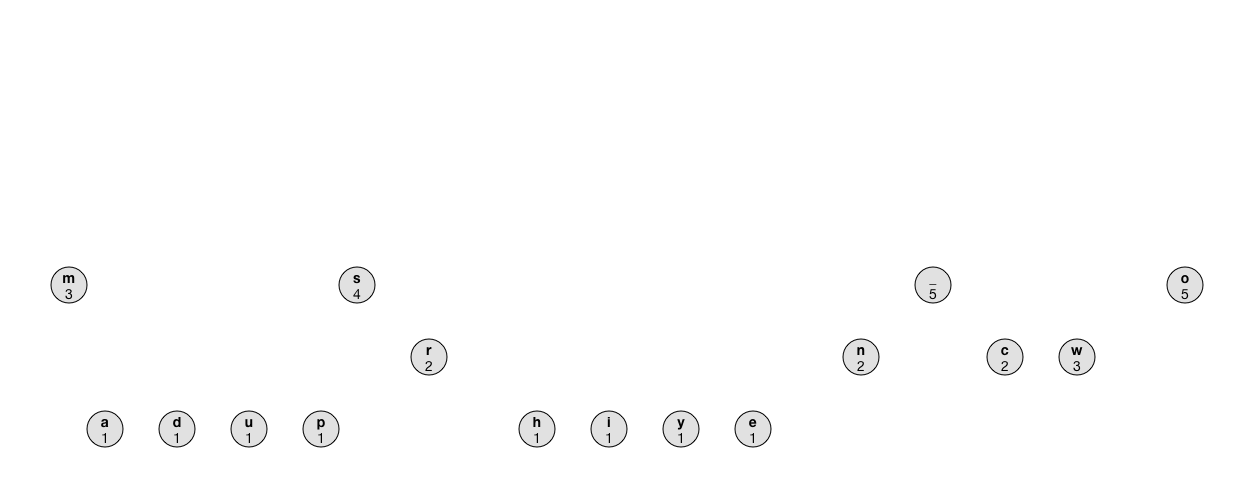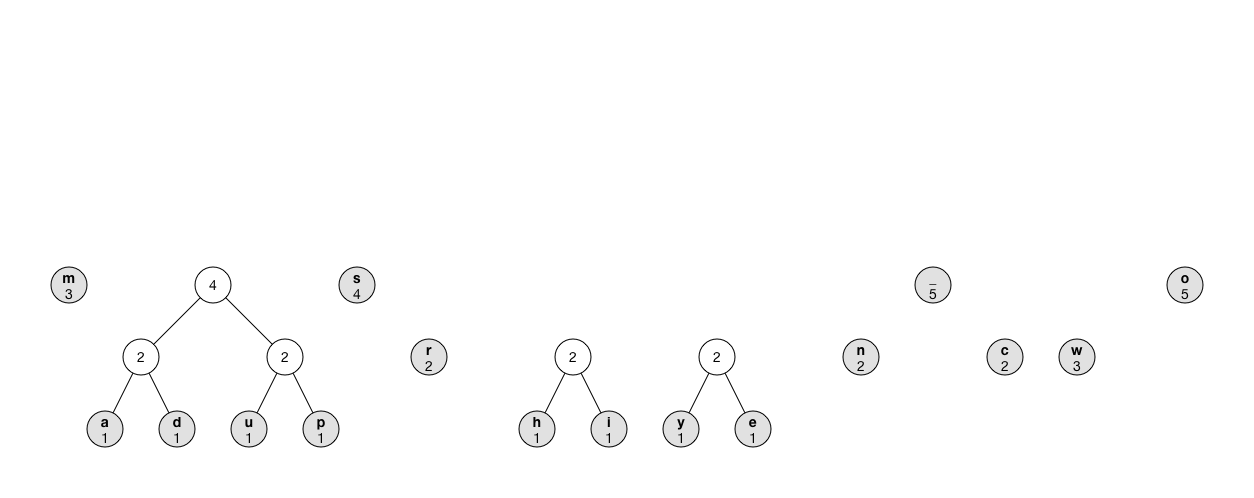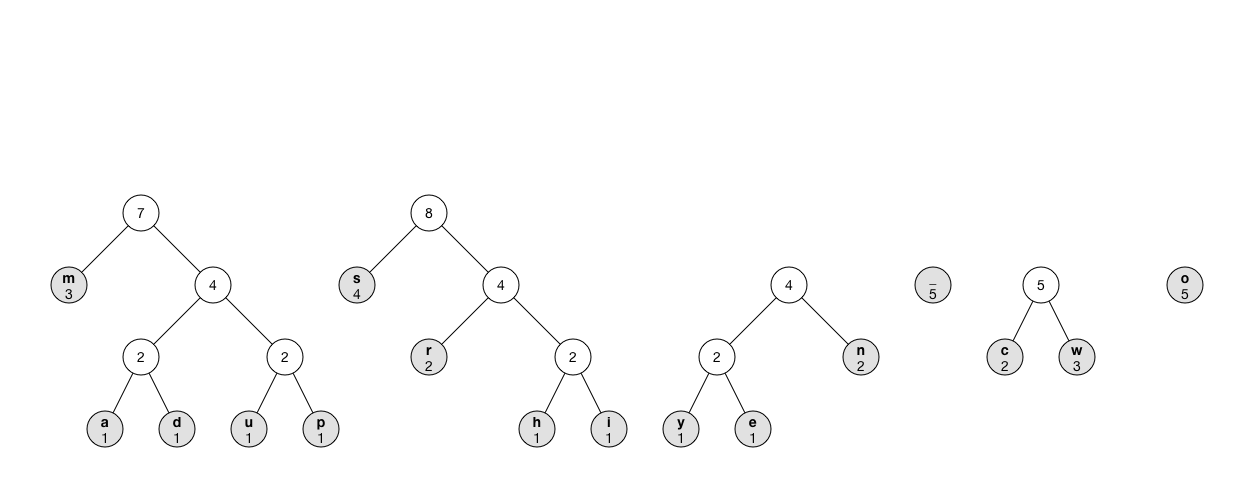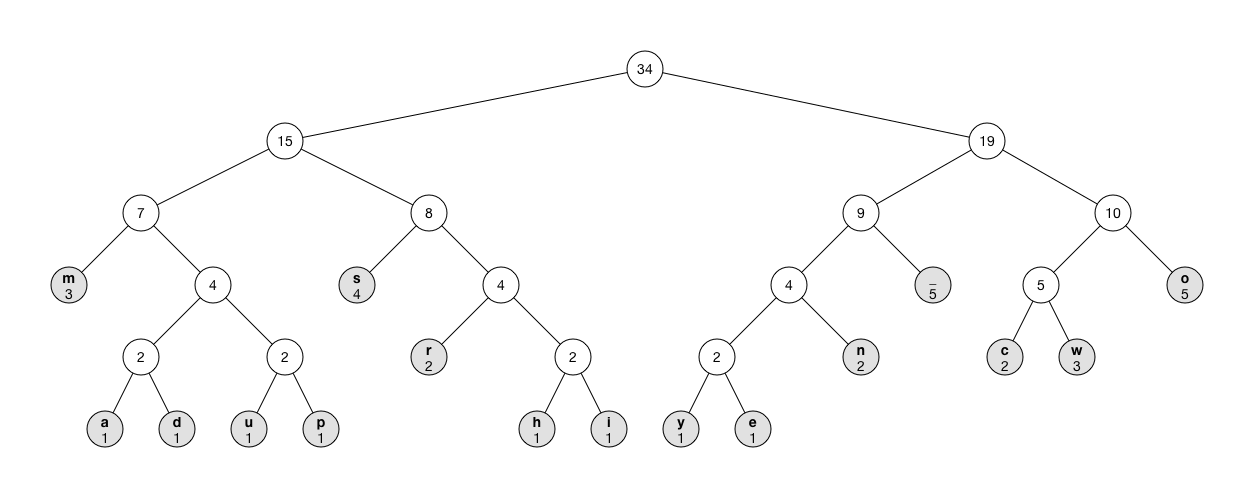
注意 除了用優先佇列(priority queue),也可以遍歷整個樹
tree陣列來找到計數值最小的兩個節點,但是這樣的時間複雜度是O(n^2),相較於時間複雜度為O(n log n)的優先佇列(priority queue)是很慢的。有趣的事實: 因為二元樹的自然特點,若有x個葉子節點,我們可以再增加最多x - 1個節點到樹中。若256葉子節點全部使用,樹的節點數最大為511個。
壓縮
接著我們可以以建立的樹來對NSData物件進行資料壓縮,實作如下:
extension Huffman {
func compressData(data: NSData) -> NSData {
countByteFrequency(data)
buildTree()
let writer = BitWriter()
var ptr = UnsafePointer<UInt8>(data.bytes)
for _ in 0..<data.length {
let c = ptr.memory
let i = Int(c)
traverseTree(writer: writer, nodeIndex: i, childIndex: -1)
ptr = ptr.successor()
}
writer.flush()
return writer.data
}
}
首先,呼叫countByteFrequency()來建立頻度表,再呼叫buildTree()來建立樹,同時建立BitWriter物件來寫入個別位元。然後以迴圈對輸入資料逐位元組呼叫traverseTree()方法,來得到每個位元組節點的路徑並寫入位元值。最後回傳BitWriter中的資料物件。
注意: 壓縮過程需要兩次遍歷整個輸入資料:第一次用以建立頻度表,第二次用以轉換成壓縮的位元編碼。
其中traverseTree()實作如下,其為一個遞迴函式:
extension Huffman {
private func traverseTree(writer writer: BitWriter, nodeIndex h: Int, childIndex child: Int) {
if tree[h].parent != -1 {
traverseTree(writer: writer, nodeIndex: tree[h].parent, childIndex: h)
}
if child != -1 {
if child == tree[h].left {
writer.writeBit(true)
} else if child == tree[h].right {
writer.writeBit(false)
}
}
}
}
當呼叫compressData()壓縮數據,要編碼的位元組,其在陣列中的索引值是為nodeIndex為葉子節點的索引值,這個方法由樹的葉節點走到根節點再回頭走一次。
當我們由根節點走回葉子節點,連接的邊是連到左子節點就寫入1的位元值,若是右子節點就寫入0的位元值。
過程圖示如下:
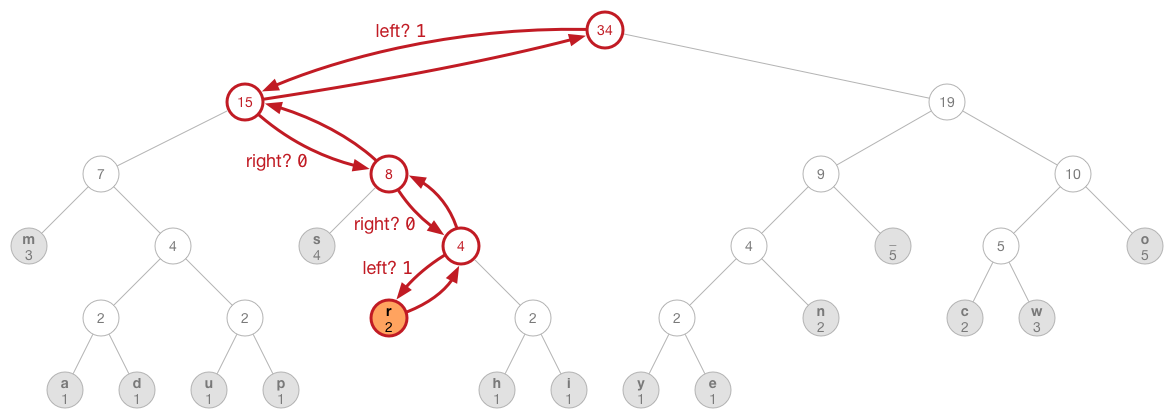
圖示中每個邊有標示0或1,實際上並沒有儲存在樹的結構中,是以路徑走的是左分支或右分支來決定值為0或1。可用下面的方式使用compressData()方法對資料進行壓縮:
var s1 = "so much words wow many compression"
if let originalData = s1.dataUsingEncoding(NSUTF8StringEncoding) {
let huffman1 = Huffman()
let compressedData = huffman1.compressData(originalData) // <a17c9c51 09d54409 7db3d18f 8975b00c>
print(compressedData.length)
}
解壓縮
解壓縮大致上就是一個壓縮的逆過程。若缺少頻度表,壓縮資料本身是無用的,先前在frequencyTable()會回傳一個Freq的物件,如果壓縮的資料存純於檔案或是透過網路傳輸,[Freq]陣列也應該一起跟隨著。首先需要將[Freq]陣列還原為樹:
extension Huffman {
private func restoreTree(frequencyTable: [Freq]) {
for freq in frequencyTable {
let i = Int(freq.byte)
tree[i].count = freq.count
tree[i].index = i
}
buildTree()
}
}
將Freq物件轉換為葉子節點再呼叫buildTree()完成剩下的部分,以下為decompressData()解壓縮函式的實作,以NSData的霍夫曼編碼(Huffman Coding)壓縮資料與頻度表作為參數傳入函式中,在回傳原始資料:
extension Huffman {
func decompressData(data: NSData, frequencyTable: [Freq]) -> NSData {
restoreTree(frequencyTable)
let reader = BitReader(data: data)
let outData = NSMutableData()
let byteCount = tree[root].count
var i = 0
while i < byteCount {
var b = findLeafNode(reader: reader, nodeIndex: root)
outData.appendBytes(&b, length: 1)
i += 1
}
return outData
}
}
此函式也用一個輔助函式來遍歷樹:
extension Huffman {
private func findLeafNode(reader reader: BitReader, nodeIndex: Int) -> UInt8 {
var h = nodeIndex
while tree[h].right != -1 {
if reader.readBit() {
h = tree[h].left
} else {
h = tree[h].right
}
}
return UInt8(h)
}
}
findLeafNode()函式以nodeIndex參數來自根節點走到葉子節點。經過每個中介節點依路徑是左是右讀取一個位元的資料(左1右0)當走到葉子節點就回傳索引值,此值相當於原資料的位元組的原始值。圖示如下:
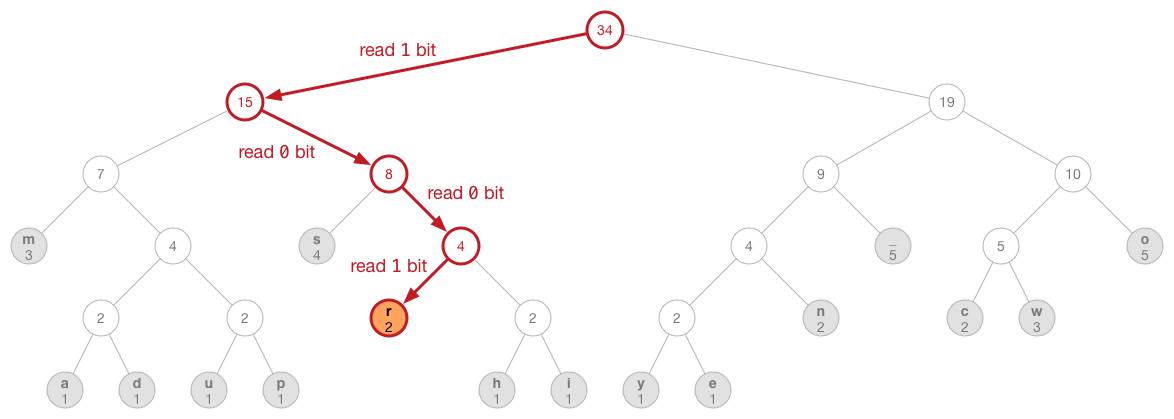
以下為如何使用解壓縮函式:
let frequencyTable = huffman1.frequencyTable()
let huffman2 = Huffman()
let decompressedData = huffman2.decompressData(compressedData, frequencyTable: frequencyTable)
let s2 = String(data: decompressedData, encoding: NSUTF8StringEncoding)!
首先取得頻度表,再呼叫decompressData()來解壓縮,解壓縮後的結果應該要跟壓縮前的資料一樣。
參考資料
測試
s1 = "so much words wow many compression"
if let originalData = s1.dataUsingEncoding(NSUTF8StringEncoding) {
print(originalData.length)
let huffman1 = Huffman()
let compressedData = huffman1.compressData(originalData)
print(compressedData.length)
let frequencyTable = huffman1.frequencyTable()
//print(frequencyTable)
let huffman2 = Huffman()
let decompressedData = huffman2.decompressData(compressedData, frequencyTable: frequencyTable)
print(decompressedData.length)
let s2 = String(data: decompressedData, encoding: NSUTF8StringEncoding)!
print(s2)
assert(s1 == s2)
}